회전을 나타내는 대표적인 방법은 3가지이다.
1. Euler Angle
개념 : x축과 y축 z축 방향으로 회전한 각도를 $\mathbb{N}^3$ 벡터로 나타낸다. roll pitch yaw
장점 : 가장 직관적으로 회전을 나타낼 수 있다.
단점 : 회전에 순서가 매겨진다. 그러므로 Gimbal lock 현상이 일어날 수 있다.
예시 :
z축 기준 $90^\circ$ 회전 후 x축 기준 $20^\circ$ 회전한 것과 y축 기준 $20^\circ$ 후 회전 z축 기준 $90^\circ$ 회전한 것이 같다.
| 서로 다른 회전이 순서를 바꾸면 같은 상태가 된다. | Gimbal lock 예시 |
 |
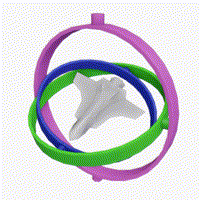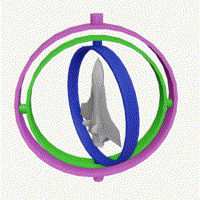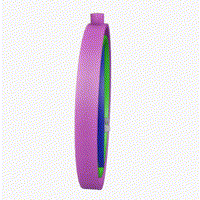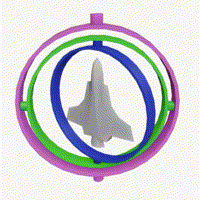 |
2. Angle axis $($rotation vector$)$
개념 : 기준축 $($reference axis$)$을 기준으로 단위 벡터$\boldsymbol u$와 회전량 스칼라 $\theta$를 통해 회전을 표현한다. Euler Angle은 Angle axis의 특수한 케이스이다. 강체의 중간에 rotation axis의 시점을 두고, xyz 방향으로 rotation vector를 그리면 Euler Angle과 똑같아진다.
장점 : Euler Angle과 다르게 순서가 없다. 또한 직관적이다.
단점 : 실제 벡터에 회전을 적용시키기 위해서는 쿼터니언이나 행렬 형태로 바꿔야 한다.
angle axis를 roataion으로 바꾸는 방법은 링크를 참조하자.
예시 :
| Angle Axis |
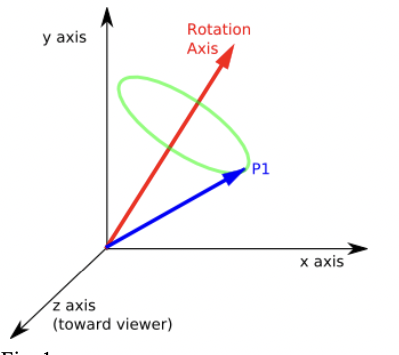 |
3. Quaternion
개념 : $p^{\prime} = q \otimes p \otimes q$으로 pure quaternion인 p의 위치를 회전시킨다.
이때 회전 시키는 q들은 unit quaternion으로
장점 : 회전의 순서가 없고, 메모리상으로도 효과적으로 회전을 구현 할 수 있다.
단점 : 직관적으로 이해하기 힘들다.
쿼터니언 회전에 대한 자세한 설명은 다른 포스트에서 확인 할 수 있다.
출처
https://stackoverflow.com/questions/9417246/quaternions-vs-axis-angle
Comments