관련 내용은
유튜브 Lie theory for the roboticist와
책 Introduction to Visual SLAM From Theory to Practice
논문 Quaternion kinematics for the error-state Kalman filter을 발췌 해서 적었습니다.

 논문의 증명 부분을 보면, 갑자기 quaternion의 회전 형태가 $ \boldsymbol{ \mathrm{x^\prime} = q \otimes \mathrm{x} \otimes q^{*}}$이라고 지르고 시작한다. 그 다음에 이 형태로 했을 때 실제 회전과 모순이 없는 것을 보인다.
 이후에 해밀턴이 어떻게 쿼터니언 회전 공식을 생각할 수 있는지 직관적 이유가 나온다. 4차원 복소 공간에서의 회전은 2차원 회전 2개로 설명할 수 있기 때문이다. 자세한 것은 논문의 2.8 Quaternion and isoclinic rotations: explaining the magic을 읽어보자.

1. quaternion $($사원수$)$

1.1 정의

복소 공간에서 허수는 회전을 나타낸다.
링크1, 링크2
링크의 유튜브 영상에서 왜 그런지 설명해 준다.

이런 허수의 성질 때문에 회전 또는 orient를 표현할 때 쿼터니언을 이용한다.
쿼터니언은 회전을 오일러의 방식 보다 간결하게 해결 할 수 있다. 또한 gimbal lock 현상도 피할 수 있다.

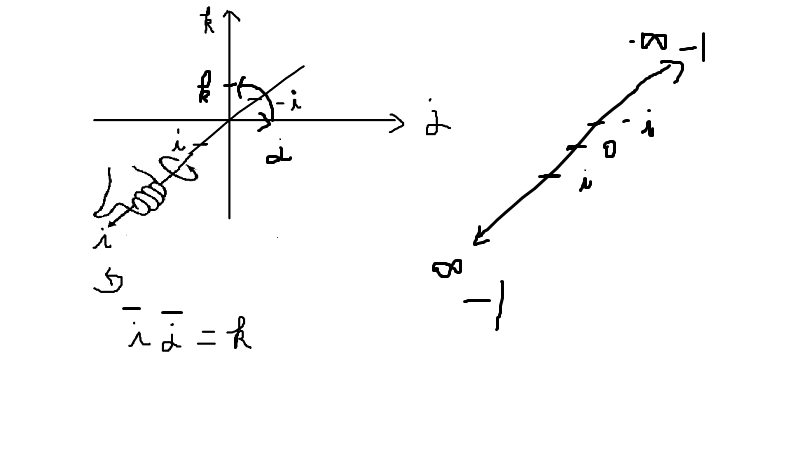왼쪽 그림을 보면 j라는 허수가 i축을 기준으로 반시계 방향으로 회전하고 있다. 이를 통해 k = i * j를 알 수 있다.
오른쪽 그림을 보면 복소 축의 infinity 값에는 -1이 대응되는 것을 볼 수 있다. ex$)$ k가 곱해질 때 마다 k, -1, -k, 0$($3차원 복소 공간에선 1이 0에 대응$)$ 로 변한다.
$k*k=-1$ 곱하면 축에서 무한대로 간다.
$ ijk=i^2=j^2=k^2 = -1 \tag{1}$ 일반적인 쿼터니언은 다음과 같이 나타낸다.
$ Q = a + bi + cj + dk \in \mathbb{H} \tag{2}$

1.2 특수한 quaternion

• pure quaternion
  $($1$)$의 식에 real part, a가 0이면 pure quaternion이다.
• normal quaternion
  l-2 norm 즉 coefficeint들의 square root 가 1이면 normal quaternion이다.
  $ \sqrt{a^2+b^2+c^2+d^2} \tag{3}$

1.3 특징

• hamilton product
  $\otimes$는 commutative 하지 않다. associative는 성립 한다. sum을 기준으로 distributable하다.
  해당 연산은 marix으로 나타낼 수 있다. 이 matirx은 skew symmetric matrix를 만족한다.

$ p \otimes q = \begin{matrix} p_w q_w - p_{v}^{T}q_v &
q_w q_v + q_wp_v + p_v \times q_v&
\end{matrix} \tag{3}$ $\times$는 cross product이다.

$[a]^T = -[a]_x\tag{4}$

matrix fomular는 다음 형태를 띈다.

\[[q]_L = \begin{bmatrix} q_w & -q_x & -q_y & -q_z \\ q_x & q_w & -q_z & q_y \\ q_y & q_z & q_w & -q_x \\ q_z & -q_y & q_x & q_w \end{bmatrix}, [q]_R = \begin{bmatrix} q_w & -q_x & -q_y & -q_z \\ q_x & q_w & q_z & -q_y \\ q_y & -q_z & q_w & q_x \\ q_z & q_y & -q_x & q_w \end{bmatrix} \tag{5}\]

identity

1이다. q * 1 = q이기 때문.

inverse

$q^{-1} = \frac{q^*}{|q|_{2}^{2}}\tag{6}$

inverse quaternion은 다음과 같이 나타난다.

$q \otimes q^* = |q|_{2}^{2} \tag{7}$

unit quaternion

inverse quaternion을 구하는 성질에 의하여, unit quaternion의 inverse는 conjugation이다. $q^{-1} = q^*\tag{8}$ 그러므로 다음과 같이 나타난다.

\[q = \begin{matrix} cos\theta & \\ u\sin{ \theta} \end{matrix} \tag{9}\]

unit quaternion은 robot의 orient나 rotatioin을 나타낼 때 쓰인다.
또한 inverse rotation이 conjugation을 통해 계산 되는 것을 알 수 있다.

product of pure quaternion, pure unit quaternion

aa

exponential of pure quaternion

natural power of pure quaternion

aa

unit quaternion의 곱은 isoclinic한 rotation을 나타낸다.

2차 복소 평면에서의 회전

실수 a b에 대한 복소 평면 위의 임의의 벡터 $\mathrm{x} = (a,bi)$의 회전은 복소 평면 위의 unit vector $z = e^{i\theta} = i \sin{\theta} + \cos{\theta}$를 이용해 구할 수 있다.
ex$)$
1,1의 정점 $\mathrm{x} = (1,i)$을 두었을 때.
이를 45^o 회전 시키면, $z = e^{45i}$를 x에 곱한다.
그려면 45^o 기울인 $(0,\sqrt2 i) = z x$ 벡터 값이 나온다.

3차원에서의 쿼터니언을 이용한 회전

위의 내용을 3차원으로 확장하면 아래와 같다.
$\boldsymbol{q} = e^{(u_x i + u_y k + u_z k)\theta /2}\tag{4}$
$ \boldsymbol{ \mathrm{x^\prime} = q \otimes \mathrm{x} \otimes q^{*}} \tag{5}$

이와 같이 오른손으로 쿼터니언의 회전을 나타낼 수 있는 쿼터니언을 hamilton quaternion이라고 한다.

Lie Algbra, Lie group

// quaternion은 회전이다.

// 한글 자료 https://alida.tistory.com/60

//image https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=seolgoons&logNo=221036574077

https://slamnerd.tistory.com/category