SCC 강한 연결 요소

15 Apr 2023 • Algorithm

강한 연결 요소

1. 활용

scc를 활용하면 2-SAT 문제나 topology sort 문제를 풀 수 있다.
2-SAT 예시 : 에타에 시간표 마법사
위상정렬 : 사이클이 있는 vertex들을 하나로 볼 수 있다.

2. 정의

하나의 방향 그래프에 여러개의 SCC가 존재할 수 있다.
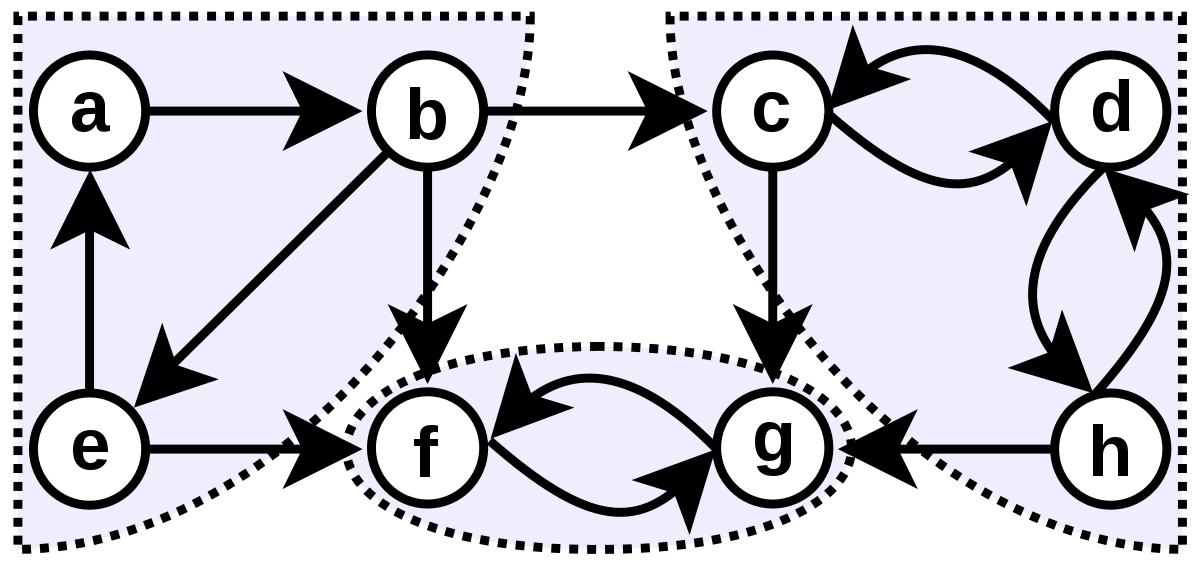SCC 그림에는 4개의 SCC가 존재한다. 여기서 주의할 부분은 c d h 정점을 하나의 scc로 보는 것이다. SCC는 큰 사이클을 이루는 정점들을 묶는다.

기억하기 쉽게 4가지 공리로 정의 해봤다.
$SCC = \{V | V\subset G, \{ v_1, v_2, \cdots, v_n \} \in V,\forall v_n \rightarrow \forall v_n, {if\ V\ containing\ overlapping\ element} \rightarrow \underset{size(V)}{\operatorname{argmax V}} \} $

  1. $V\subset G$
    directect graph의 vertex로 이루어진 집합이다.
  2. $\{ v_1, v_2, \cdots, v_n \} \in V$
    vertex들을 다음과 같이 나타낸다고 하자.
  3. $\forall v_n \rightarrow \forall v_n$
    SCC안의 임의의 정점은 임의의 정점으로 이동할 수 있다.
    이것이 strongly connected 조건이다.
  4. ${if\ V\ containing\ overlapping\ element} \rightarrow \underset{size(V)}{\operatorname{argmax V}} $
    서로 다른 SCC를 이루는 정점들이 겹칠 때, 큰 사이즈의 집합을 선택한다. 위 그림의 c d h 정점이 예시이다.
    이 조건이 cycle과 scc 정의의 차이점이다.
    $SCC \rightarrow cycle$은 성립하나,
    $cycle \rightarrow SCC$은 성립하지 않는다.

3. 구현

scc 문제는 두가지 알고리즘으로 풀 수 있다.
타잔 알고리즘과, 크루스칼 알고리즘이다.
아래는 타잔 알고리즘이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

// 2150번 tarjan algorithm
#include <bits/stdc++.h>
using namespace std;
int V, E;
vector<vector<int>> SCC;
vector<int> graph[10001];
int visit_sequence[10001];
int start_sequence = 0;

bool finished[10001];

stack<int> stack_buffer;

bool comp_first(const vector<int>& l, const vector<int>& r){
    return l[0] < r[0];
}

int updateLowLinkValue(int here){
    visit_sequence[here] = ++start_sequence;
    stack_buffer.push(here);
    int low_link_value = visit_sequence[here];
    for(int there: graph[here]){
        if(visit_sequence[there] == 0)
            low_link_value = min(low_link_value, updateLowLinkValue(there)); // 4번 공리를 만족 시키기 위해 
        else if(!finished[there])
            low_link_value = min(low_link_value, visit_sequence[there]); // 이미 scc가 된 원소는 무시한다. if(finished[there]) continue;로 해도 됨.
    }

    // 부모 노드가 자기 자신인 경우
    if(low_link_value == visit_sequence[here]){
        vector<int> scc;
        while(1){
            int t = stack_buffer.top();
            stack_buffer.pop();
            scc.push_back(t);
            finished[t] = true;
            if(t == here) break;
        }
        SCC.push_back(scc);
    }
    return low_link_value;
}

void update_scc(){
    for(int i = 1; i <= V; i++)
        if(visit_sequence[i] == 0)
            updateLowLinkValue(i);
}

int main(){
    cin.tie(nullptr);
    cout.tie(nullptr);
    ios_base::sync_with_stdio(false);

    cin >> V >> E;
    while(E--){
        int t1, t2;
        cin >> t1 >> t2;
        graph[t1].push_back(t2);
    }

    update_scc();
    
    if(!SCC.empty())
        cout << SCC.size() << "\n";

    for(auto &scc : SCC)
        sort(scc.begin(), scc.end());
    sort(SCC.begin(),SCC.end(), comp_first);
    
    for(auto scc_ : SCC){
        for(int elem: scc_){
            cout << elem << " ";
        }
        cout << "-1 \n";
    }
}

24번째 줄이 4번째 공리, 가장 큰 cycle을 찾기 위해 가장 작은 low_link_value를 찾는 것이다.
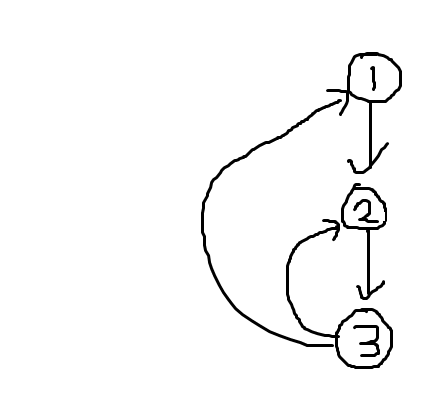axiom4 위 그림과 같이 3번째 노드에서 2번째 노드를 방문하고 1번 노드를 방문하는 경우, 24번째 줄이 필요하다.

  • directed graph에는 유한개의 scc가 유일하게 존재 한다.
  • 모든 그래프 전체가 scc가 될 수 있다.
    undirected라면 모든 graph가 scc다.
 Graph  SCC

Comments

Related Posts